

You can also check out my lattice method of multiplication worksheet below. If you find this method useful, leave me a comment and let me know! Check out my video above as I walk you through a few examples of how it is performed. The lattice method is fairly easy to use once you know how it works.
Lattice method multiplication how to#
How To Perform Multiplication Using The Lattice Method Despite the fact that both procedures involve breaking out the numbers, multiplying them, and then putting them together, there are some significant changes in the way they’re written down. 1 The multiplicand is the first number in a multiplication operation while the multiplier is the last number. The number a corresponds to the number of digits of the multiplicand (number being multiplied) and b to the digits of the multiplier (number doing the multiplying). The lattice method of multiplication is a different approach to long multiplication than the formal written method. Steps 1 Draw a table with a x b number of columns and rows, respectively. It is mathematically identical to the more commonly used. This is also a valuable multiplication approach since it gives students a model to follow to verify that the numbers are aligned correctly. Lattice multiplication, also known as the Italian method, Chinese method, Chinese lattice, gelosia multiplication, sieve multiplication, shabakh, diagonally or Venetian squares, is a method of multiplication that uses a lattice to multiply two multi-digit numbers. This can assist students in seeing the many procedures and better understanding how to multiply numbers. This is a useful way for breaking large numbers down into simple math. However, it can also be applied to bigger multi-digit figures. It’s typically utilized when multiplying two-digit integers by two-digit numbers. Lattice multiplication, often called Chinese multiplication, is a way of multiplying integers. What Is The Lattice Method Of Multiplication?
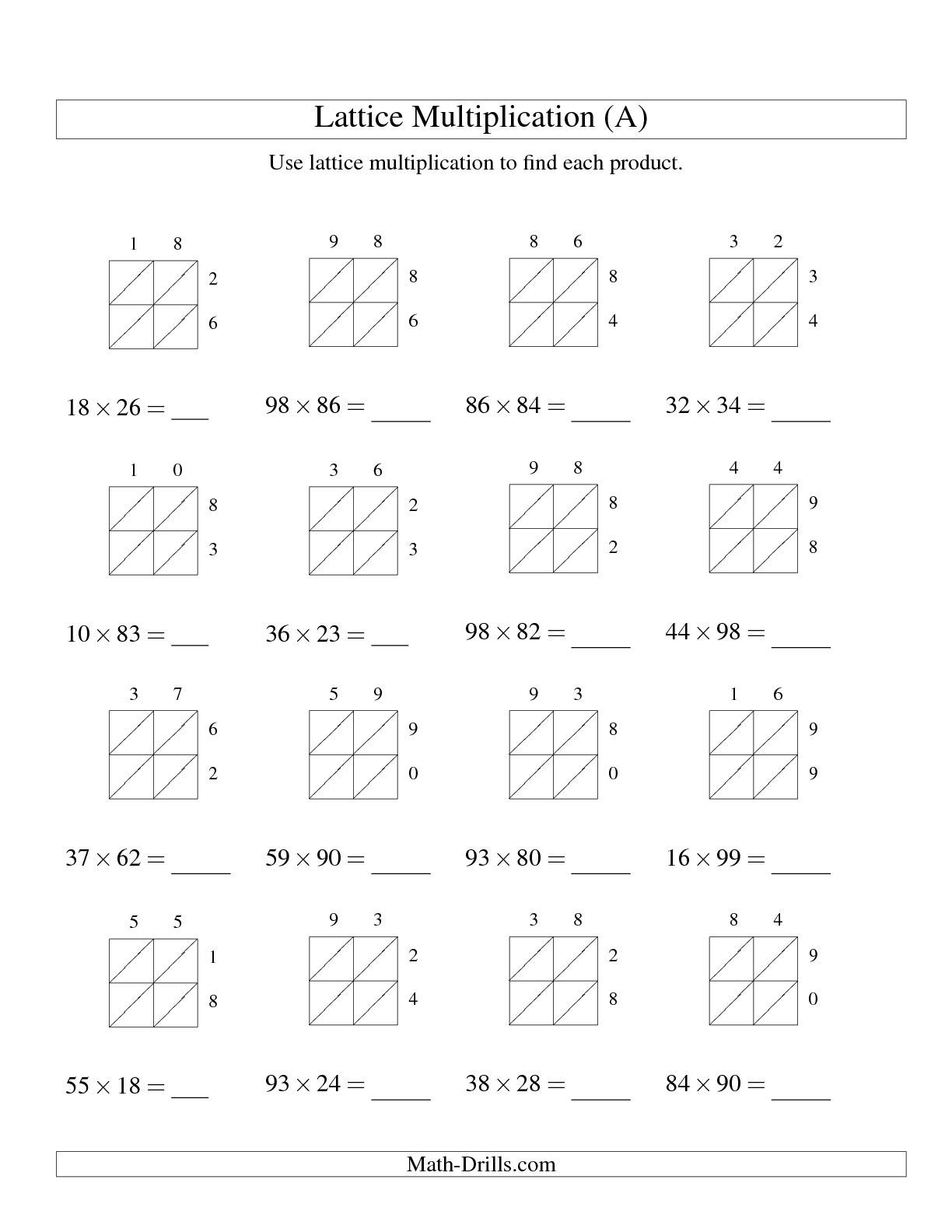
The lattice method of multiplication is an alternative way to multiply multi-digit numbers.


 0 kommentar(er)
0 kommentar(er)
